Huang X, Belongie S. Arbitrary style transfer in real-time with adaptive instance normalization[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 1501-1510.

1. Overview

In this paper, it proposes a Adaptive Instance Normalization (AdaIN) motivated by Instance Normalization (IN).

2. Normalization

2.1. Barch Normalization (BN)

For $x \in R^{N \times C \times H \times W}$.
1) $BN(x) = \gamma (\frac{x - \mu (x)}{\sigma (x)}) + \beta$.
2) $\mu_c (x) = \frac{1}{NHW} \sum_{n=1}^{N} \sum_{h=1}^H \sum_{w=1}^W x_{nchw}$
3) $\sigma_c(x) = \sqrt{\frac{1}{NHW} \sum_{n=1}^{N} \sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_c(x))^2 + \epsilon}$
4) $\gamma, \beta$ are learnable parameters.
BN uses mini-batch statistics during traning and replace them with popular statistics during inference, introducing discrepancy between training and inference.

2.2. Instance Normalization (IN)

1) $IN(x) = \gamma (\frac{x - \mu(x)}{\sigma(x)}) + \beta$.
2) $\mu_{nc}(x) = \frac{1}{HW} \sum_{h=1}^H \sum_{w=1}{W} x_{nchw}$.
3) $\sigma_{nc}(x) = \sqrt{\frac{1}{HW} \sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_{nc}(x))^2 + \epsilon }$.

No discrepancy during inference.

2.3. Conditional Instance Normalization (CIN)

Instead of learning a single set of affine parameters $\gamma, \beta$, CIN learns a different set of parameters $\gamma^s, \beta^s$ for each styles $s$.
1) $CIN(x;s) = \gamma^s (\frac{x - \mu(x)}{\sigma(x)}) + \beta^s$

2.4. Interpreting Instance Normalization (IN)

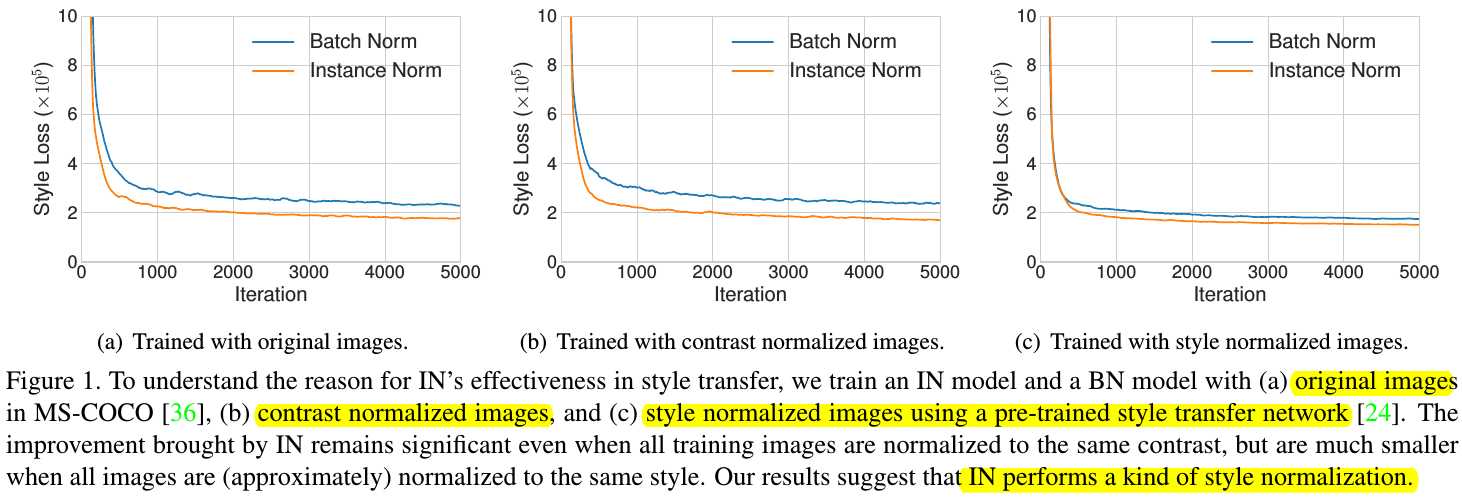
1) Argue that IN performs a form of style normalization by normalizing feature statistics.
2) Believe that feature statistics of a generator network can also control the style of the generated image.

3. Adaptive Instance Normalization (AIN)

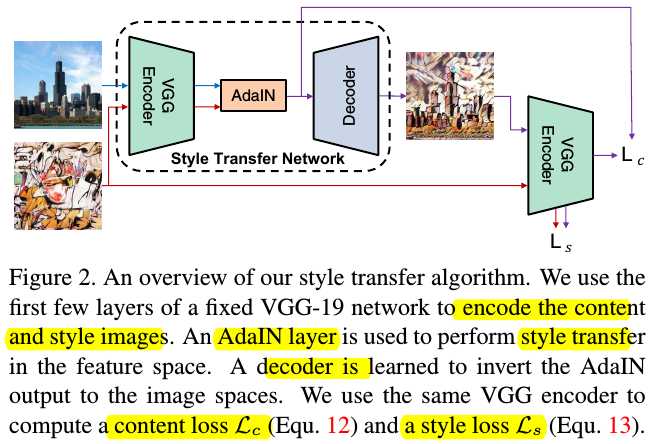
3.1. Details

$AdaIN(x,y) = \sigma(y) (\frac{x - \mu(x)}{\sigma(x)} ) + \mu(y)$.
1) Content input $x$ and style input $y$.
2) Simple scale the normalized content input with $\sigma(y)$ and shift it with $\mu(y)$.
3) No learnable affine parameters.

$T(c,s) = g(t)$.
$t = AdaIN(f(c), f(s))$.

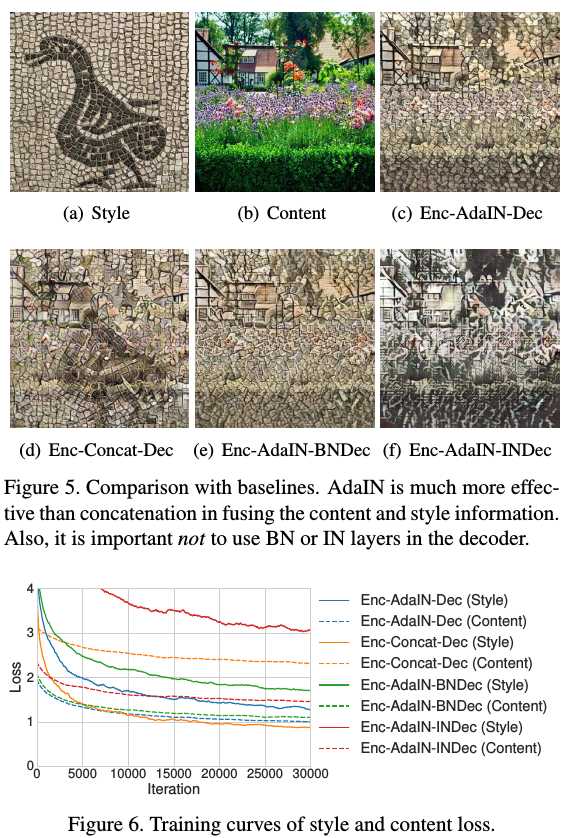
1) IN normalizes each sample to a single style while BN normalizes a batch of samples to be centered around a single style. Both are undesirable when want the decoder to generate images in vastly different styles.
2) Thus, do not use normalization layers in the decoder.

3.2. Loss Function

1) $L = L_c + \lambda L_s$.
2) $L_c = || f(g(t)) - t||_2$.
3) $L_s = \sum_{i=1}^L || \mu(\phi _{i} (g(t))) - \mu (\phi_i(s))||_{2}+\sum _{i=1}^L|| \sigma(\phi _{i} (g(t))) - \sigma( \phi_i (s)) || _2$.

4. Experiments

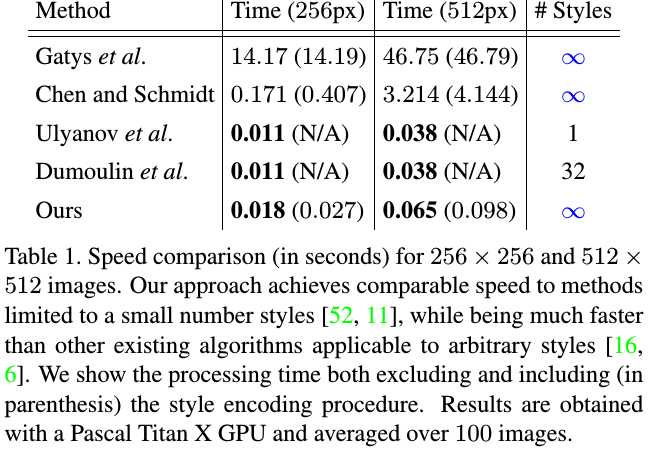
4.1. Speed

4.2. Ablation Study

4.3. Content-style Trade-off

$T(c, s, \alpha) = g( (1 - \alpha) f(c) + \alpha AdaIN(f(c), f(s)) )$

4.4. Style Interpolation

$T(c, s_{1,2,…,K}, w_{1, 2, …, K}) = g(\sum_{k=1}^K w_k AdaIN(f(c), f(s_k)))$

4.5 Color Control

1) Match the color distribution of the style image to that of the content image
2) Perform a normal style transfer using the color-aligned style image as the style input.

4.6. Spatial Control

Perform AdaIN to different regions.